Model Merging: Combining Different Fine-Tuned LLMs
By Ignacio Aristimuño
Model Merging
1. Introduction
Model composition is a well-known problem in the Machine Learning community. Its aim is to extend the capabilities of a model, without forgetting what it already knows. Let’s consider a situation in which we have a good performing model in a certain task (e.g. Text-to-SQL) but it was fine-tuned for that specific task, losing part of its ability to do other tasks such as summarization or translation. There are many techniques for adding new skills to a model, such as fine tuning, active learning, ensemble models and model soups. However, this becomes especially important in today’s AI context due to the impact of these techniques applied to Large Language Models (LLMs). That’s were Model Merging comes into play.
Some of the most relevant approaches when talking about LLMs are: Mixture-of-Experts (MoE), Model Merging and Block Expansion. We will go through some basic notions of all three and deepen into model merging, but on a high level:
- Mixture-of-Experts (MoE): consists of using several models (called experts) and training a gating network (usually called router) that selects the most appropriate experts to answer a question or complete an instruction.
- Model merging: is a process where, usually, the weights of different models with the same architecture (which can also be called experts) go through a merging operation (e.g. interpolation) to create a new single model. However, some merges can involve stacking layers of different models without altering their weights.
- Block expansion: consists of adding blocks of transformations fine tuned in new data to extend the capabilities of the model.
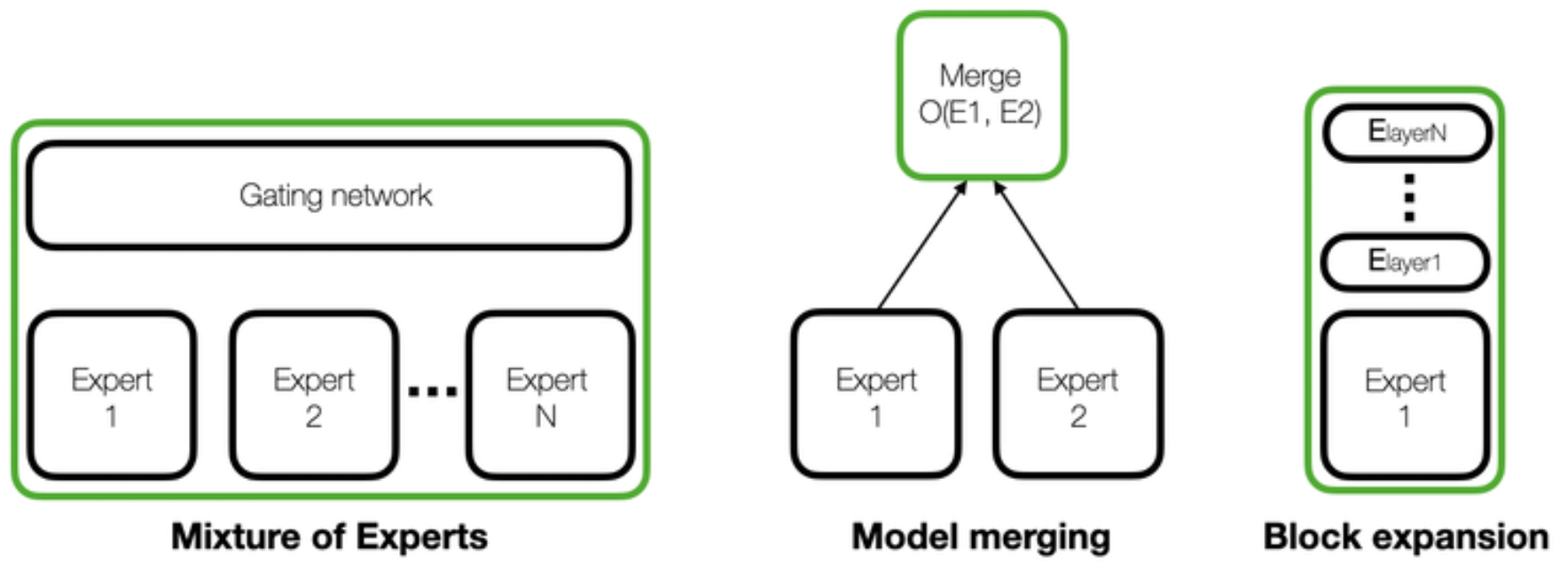
Schema of three popular methods to expand the skills of LLMs. The resulting model is shown within a green box [1].
1.1 Mixture-of-Experts
This architecture was presented in Switch Transformers paper [2]. However, it has recently gaining a lot of attention due to two main events. Firstly, there were some comments from reliable people of the AI community, such as George Hotz, claiming that GPT-4 was an eight-way MoE model with about 220B parameters. Moreover, the release of Mixtral [3] gained a lot of attention, becoming one of the most popular non-proprietary LLMs by the community.
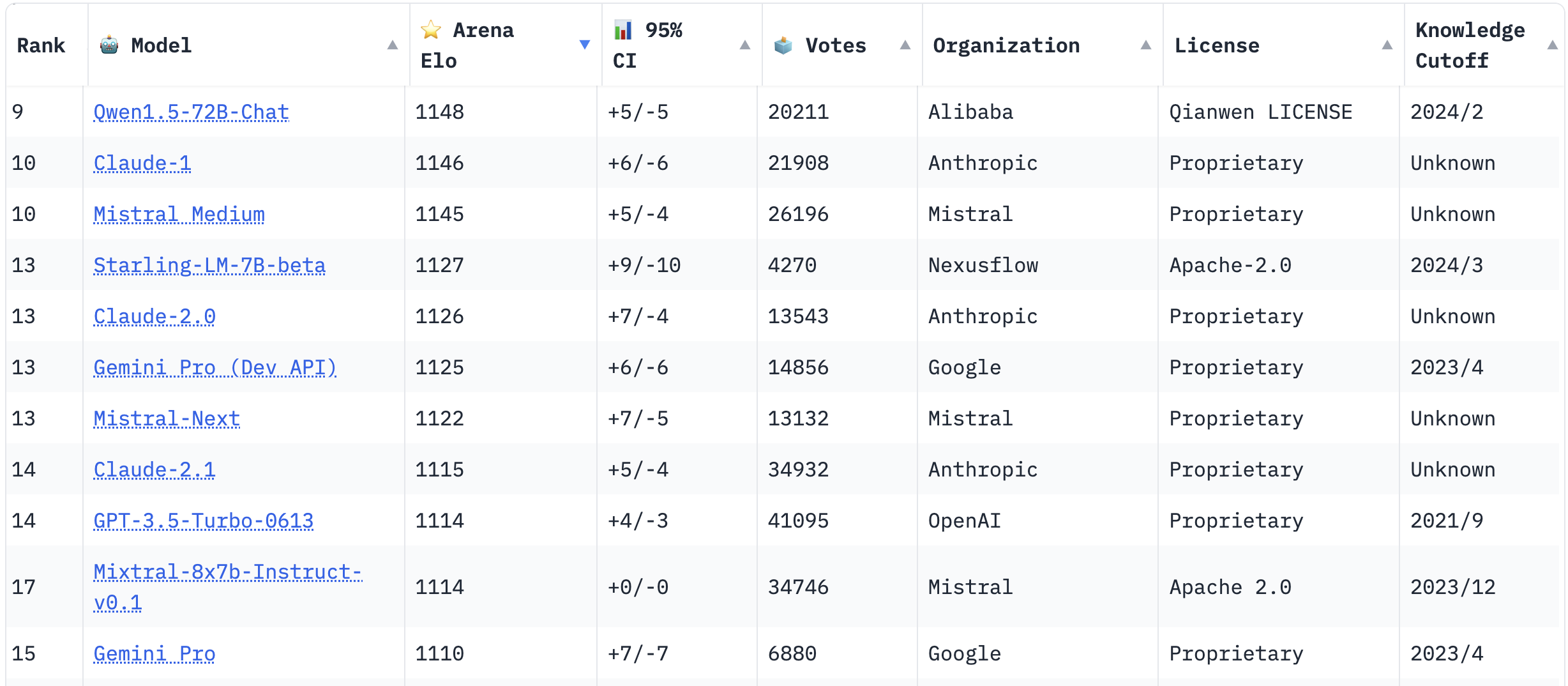
Most popular LLMs voted by the community in March 2024. Starting at index 9 to show Mixtral within the table [4].
Let’s exemplify how MoEs work, talking specifically about Mixtral. Mixtral is a decoder-only transformer model that groups a router (or gating network) and 8 different parameters sets (experts). For each input prompt, Mixtral’s router selects two experts at each layer and token, and combines their outputs additively. Training happens simultaneously for both the router network and the experts.
This approach outperformed bigger LLMs such as LLaMA 70B (v1) and GPT 3.5 in most benchmarks. Furthermore, the total amount of parameters is 46.7B (8 experts) and it uses only 12.9B (2 experts) per token during inference. This means a x6 faster inference boost in comparison to single models of the same size.
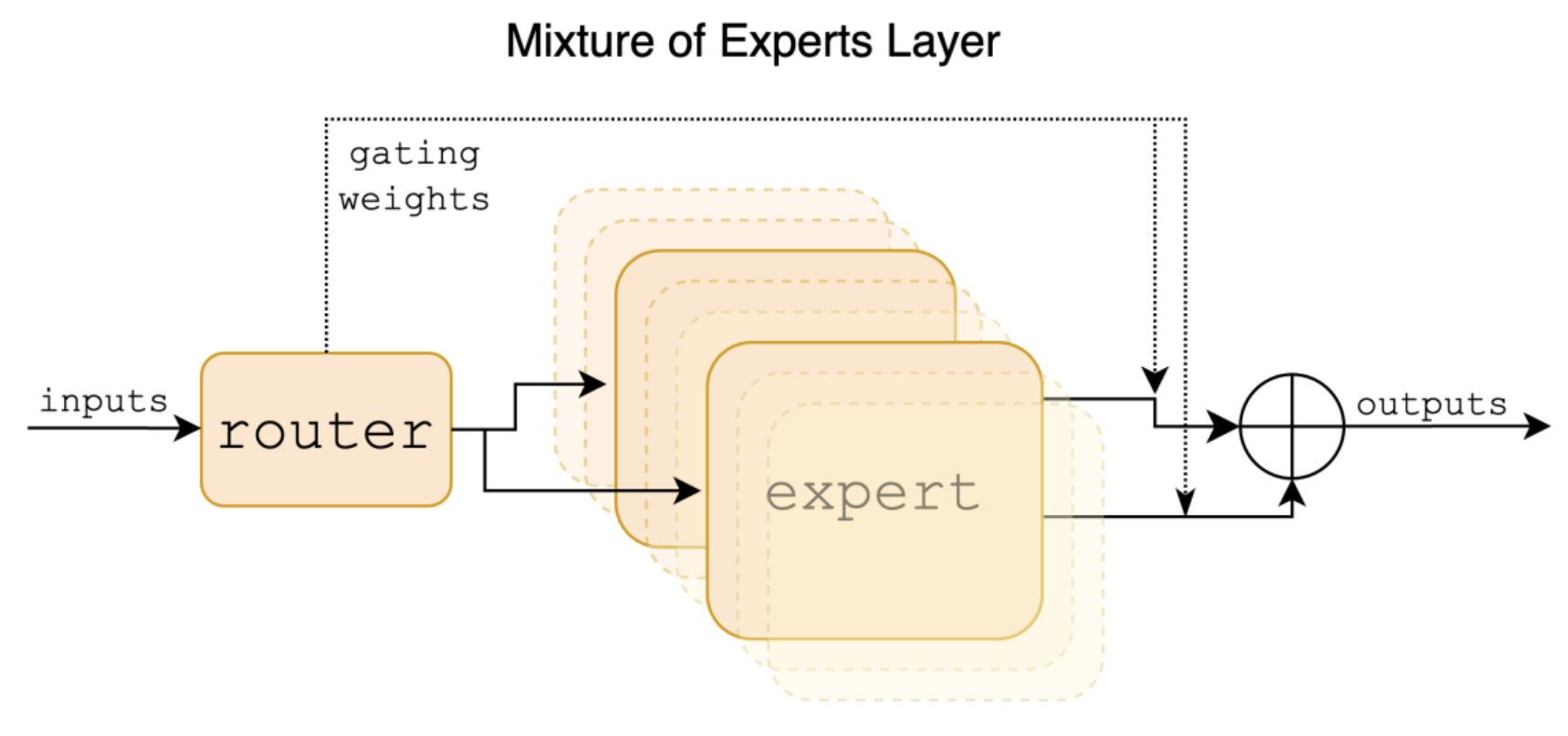
Schema representing Mixtral’s sparse MoE architecture [5]
1.2 Block expansion
This concept is relatively new, although there several similar approaches such as Low-Rank Adaptation (LoRA) and HyperNetworks for both LLMs and Diffusion models . Some examples of these can be found in our blog on Teaching Diffusion Models Specific Concepts.
In order to add new capabilities to an existing model without compromising its performance on already known tasks, we iteratively add new transformers blocks trained on these new tasks while freezing the previous blocks. The major drawback of this technique is the increase in model memory consumption and higher latency during inference.
2. Why merging models?
Short answer: model merging is easy. There’s no need for fine tuning or adding new trainable layers to the selected models. Moreover, there are efforts by the open-source community to develop tools to facilitate these tasks, such as model merging. This makes the adoption of these techniques even easier. Probably, the most popular library at the moment for model merging is mergekit [6].
Merging takes a lot of trial and error, but does not take fancy clusters or labs for leveraging a big compute power.
Until recently, merging models with different architectures or sizes (e.g Mistral and LLaMA v2) was not possible. Nevertheless, this approach is becoming more common, especially with the release of some frankenmerges such as SOLAR 10.7B and Goliath 120B.
2.1 LLM Leaderboards
Also, let’s have a look at the Open-LLM Leaderboard, taking out the fine tuned on specific datasets and chat models.
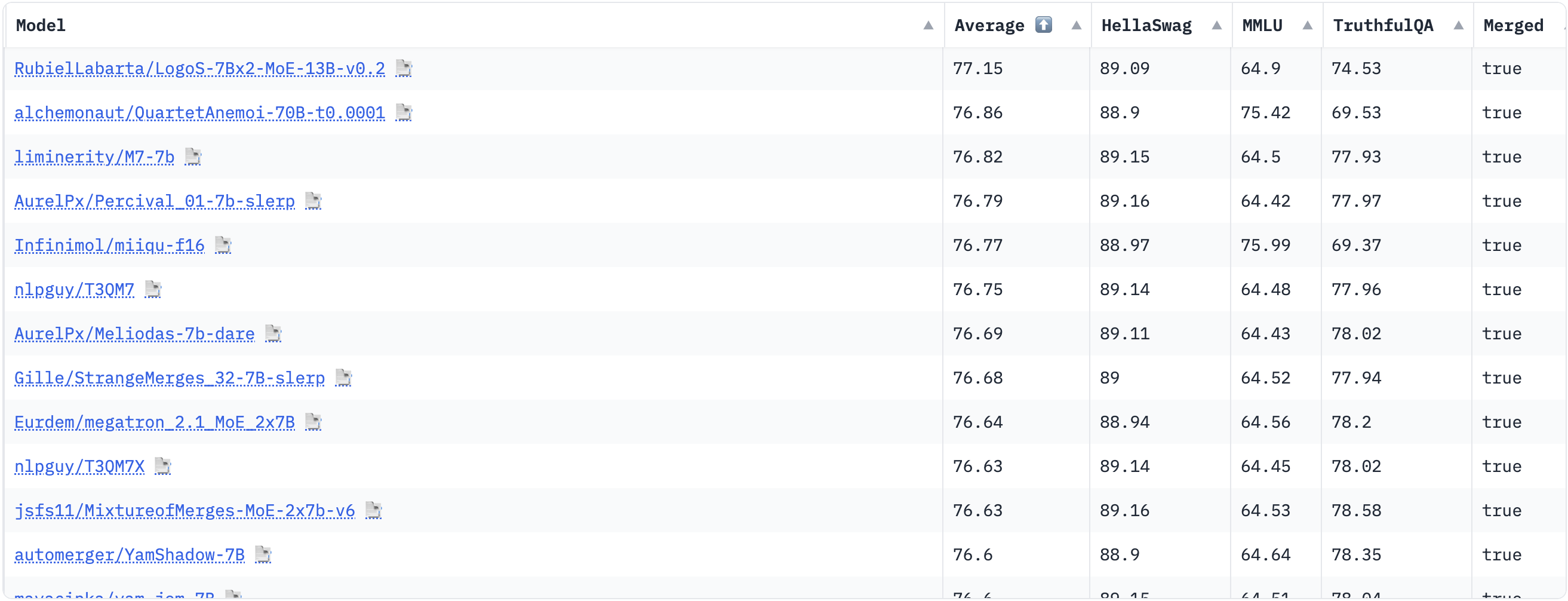
Top performing models in the Open-LLM Leaderboard.
It may be surprising to see that the top performing models doesn’t seem familiar. Although, this phenomenon does not happen when looking at other leaderboards such as the LMSYS Chatbot Arena Leaderboard. This is due to two main reasons. First, model merging and other types of merging such as FrankenMoEs (merging models through creating MoEs) are becoming more and more popular. This increases the number of models in the Open LLM Leaderboard significantly. As we can see in the last column of the table, top performing models are all merges up to March 2024. Also, as these merges can enhance the performance of the models in certain tasks, these could be even better than the models used as input for merging, hence the high scores in the evaluation datasets.
Second, some of these merges are using models which have used data from the test set of evaluation benchmarks. Indirectly, this is making them perform incredibly high on these benchmarks, as they have information leakage. This dos not happen in the Chatbot Arena Leaderboard, as the maintainers select which models to evaluate.
3. Merging methods
Although there are several methods to merge models, we will focus on three of the most popular alternatives. Also, this handpicked selection was made to show different approaches and not similar ones as they slightly vary between each other (such as linear interpolation and spherical linear interpolation).
The three methods which we will describe within this section are:
- Spherical Linear Interpolation (SLERP)
- Task Vector Algorithms
- Frankenmerging (also known as Frankenstein merges or Passthrough)
On the other hand, there is also the option of merging through the creation of a MoE model (also known as FrankenMoEs), blending expertise for better performance. However, this is out of the scope for this blog.
3.1 SLERP
This technique consists of smoothly blending two models by navigating through the shore path on a high-dimensional sphere. For the sake of simplicity let’s consider we are merging four weight vectors with only two positions, which we will show on a 2D plane for better visualization.
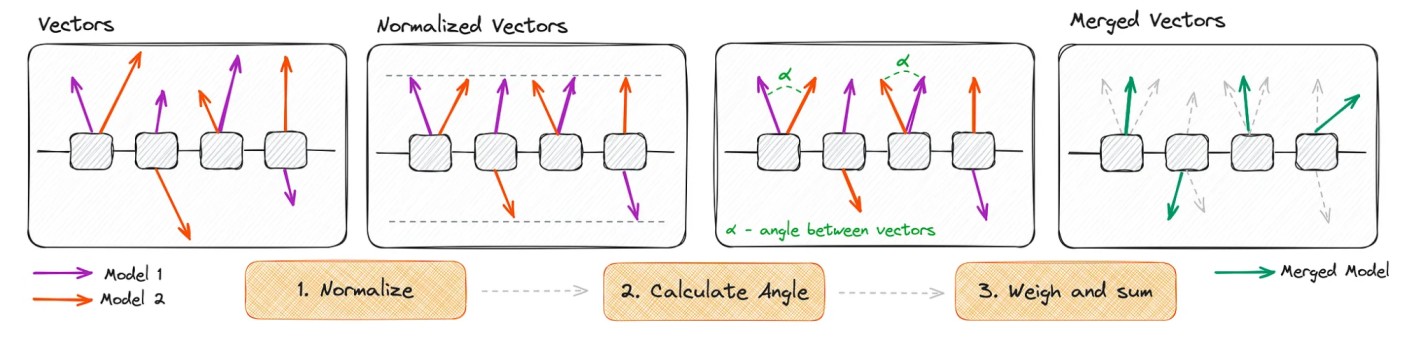
Schematic illustration of the SLERP algorithm [7]
The steps involved in SLERP are as follows:
- Normalization: normalizing the vectors for having the same length.
- Angle calculation: calculate the angle (theta or alpha) in radians between these vectors.
- New vector calculation: calculate the a the new vector (v1+2) following the formula which is shown below.
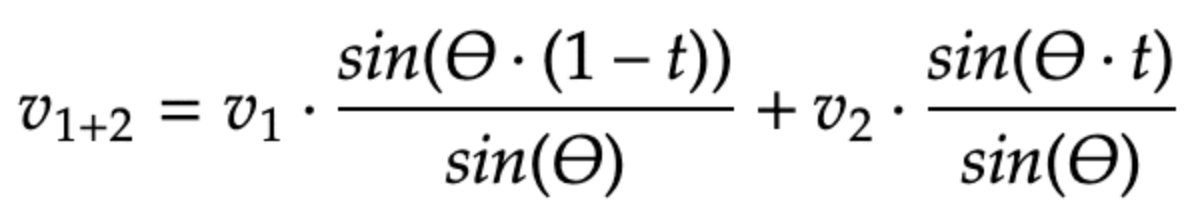
Formula for new vector calculation with the SLERP algorithm [11]
In this formula, the parameter t ∈ [0, 1] refers to a weight applied for both models. When t=0, only Model 1 is used, and when t=1, only Model 2 is used.
SLERP improves on standard weight averaging by maintaining each model’s unique characteristics and curvature, even in intricate, high-dimensional spaces.
3.2 Task Vector Algorithms
This method introduces a new paradigm for modifying the behavior of neural networks using task vectors. These vectors represent directions in the weight space of a pre-trained model, pointing towards improved performance on a specific task. By using arithmetic operations like negation and addition, we can manipulate vectors, making behavioral changes in the model. This idea was introduced in the paper “Editing Models with Task Arithmetic” [8].
Tasks vectors are computed by subtracting the weights of a base model from the weights of a task-specific model that has been fine-tuned based on that same base model. Unlike SLERP, we can merge several models at once.
3.2.1 Task vector operations
The most common operations are as follows:
- Forgetting via negation: negating a task vector diminishes the model’s performance on the target task while maintaining its behavior on control tasks. This can be especially useful for bias mitigation or in cases where we want to keep data privacy (e.g. forgetting memorized private information).
- Learning via addition: adding task vectors can enhance the model’s performance across multiple tasks simultaneously.
- Task analogies: combining task vectors from related tasks (based on an analogy relationship) can improve performance on a fourth task, even without using data from this task. This is achieved using analogies such as: “A is to B, as C is to D”, where A, B and C are already learned tasks and D is a task which was not seen (or almost not seen) during training.
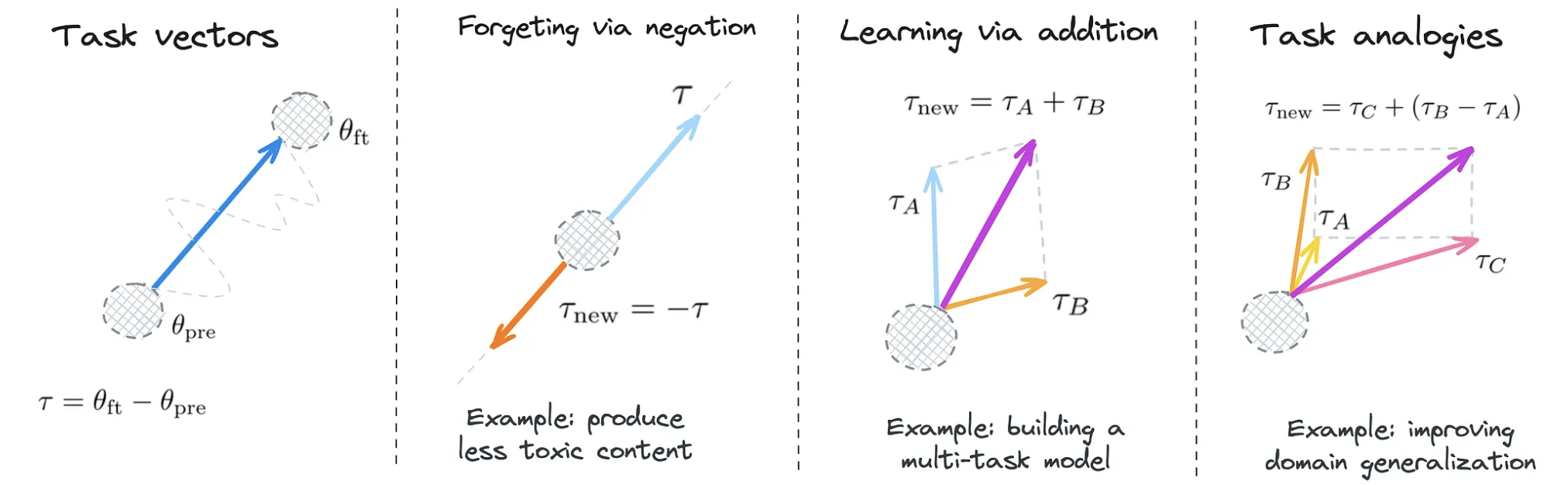
Schema representing the most common arithmetic operations on task vectors [7]
3.2.2 Most common algorithms
There are four main task vector algorithms in mergekit [6]
- Task Arithmetics: which focuses on calculating task vectors and adding the results to the base model weights. [9]
- TIES: was designed to efficiently merge multiple task-specific models into a single multitask model. It addresses redundancy in model parameters (ignoring small weight changes) and disagreement between parameter signs. [10]
- DARE: it’s similar to TIES but with two main differences: pruning by randomly reseting fine-tuned weights to the base model, and rescaling weights. [10]
- DARE + TIES: combines the redundancy approach of TIES with the rescaling of DARE.
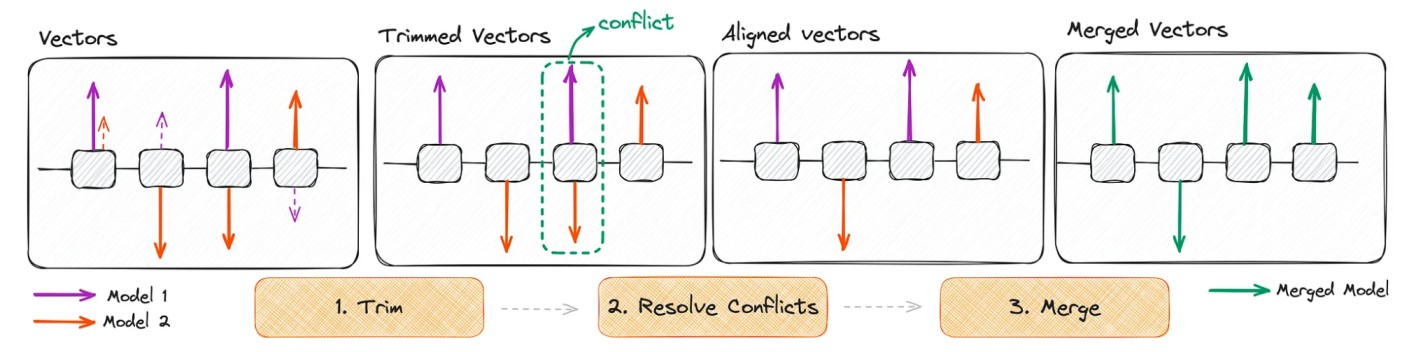
Schematic illustration of the TIES algorithm [7]
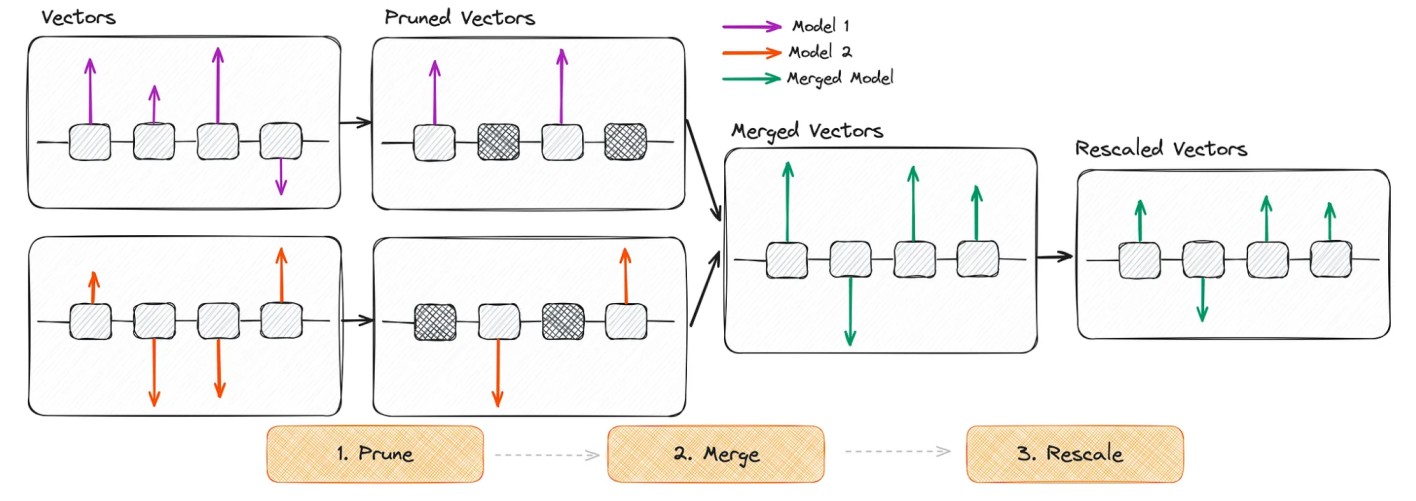
Schematic illustration of the DARE algorithm [7]
3.2.3 Algorithms comparison
A quick comparison for guiding into which task vector algorithm suits best to your use case is shown in the table below:
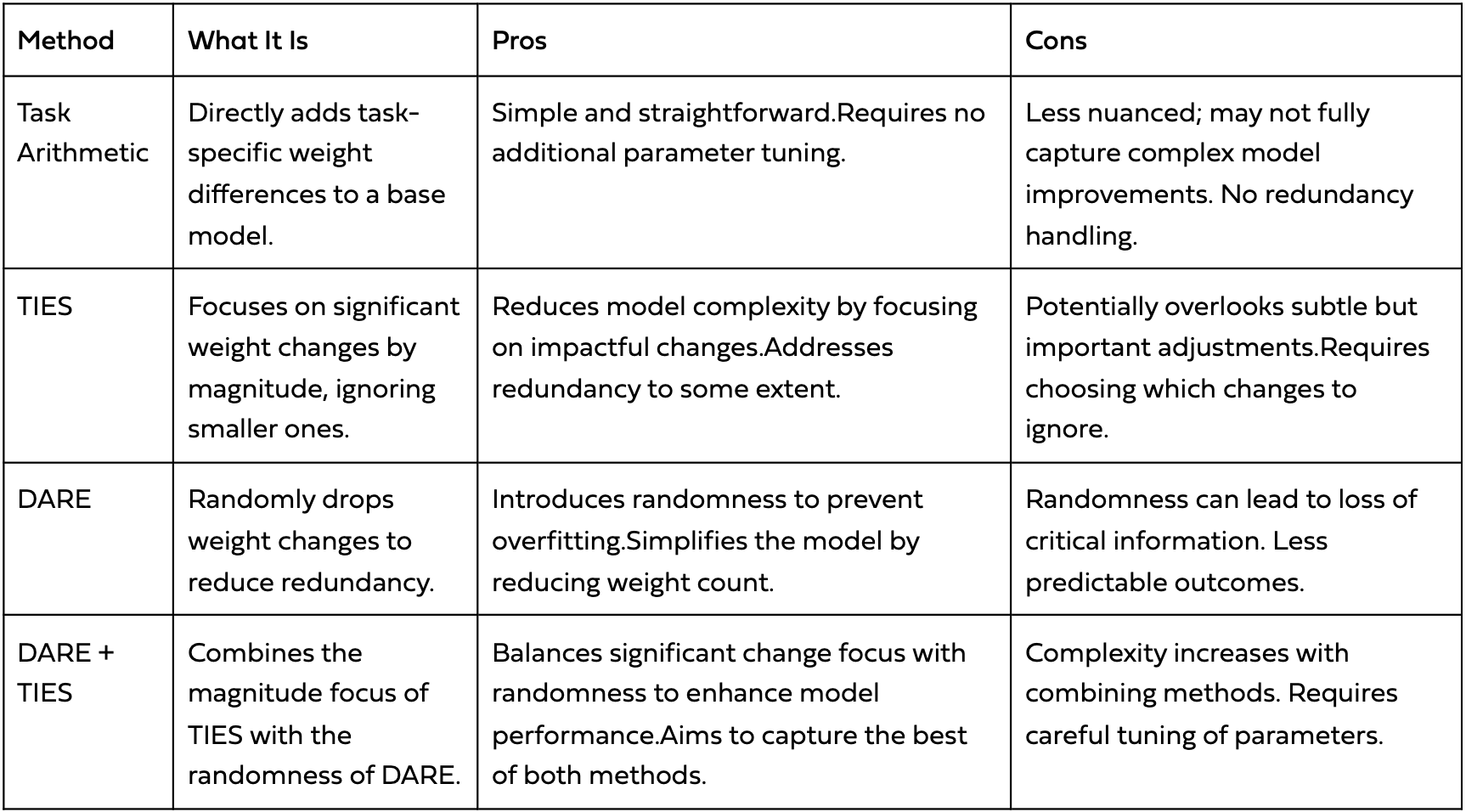
Comparison of pros and cons of different task vector algorithms [11]
3.3 Frankenmerging
This technique involves the process of merging different models by mixing pieces of them together. More specifically, stacking different layers sequentially instead of fusing different layers. Currently, this is one of the two methods in mergekit that works for different model architectures. This method can also be found as Passthrough or Frankenstein models. The other method common method in the community is FrankenMoEs, which applies this frankemerging idea but using the MoE architecture. For more information about these, check the mlabonne/Beyonder-4x7B-v2 model which is a clear example of this.
Frankenmerging can produce models with an exotic number of parameters (e.g. 9B merged model based on two 7B models). Although it’s still quite an experimental technique, but the community is getting impressive results with it. It requires a lot of trial and error as there is no formula for achieving the optimal merge.
4. Merging your own models
In this section, we will provide an overview of how to leverage mergekit to create your own merged models. This process consists essentially of loading a merge configuration file and running it. As simple as it sounds.
In this blog we will show how to use the DARE-TIES merge using different math-focused models from the same family (Mistral 7B). Afterwards, we will evaluate our final model in the GSM8K dataset, which consists of 8.5K high quality linguistically diverse grade school math word problems created by human problem writers. The idea is to comparte the individual models to our merge.
4.1 Installation
For installing mergekit just install the library through pip install or install from source
git clone https://github.com/cg123/mergekit.git cd mergekit && pip install -q -e .
Then, we should create the configuration files to define the merge we want to do.
4.2 DARE-TIES with mergekit
For identifying which models come from the same family tree, Maxime Labonne created this awesome tool: Model Family Tree. Although, by lookin at the model cards in the Hugging Face hub you can usually track its precedence.
In this demo, we are using mistralai/Mistral-7B-v0.1 as the base model and we will be merging two math models from the same family: meta-math/MetaMath-Mistral-7B and WizardLM/WizardMath-7B-V1.1. We are defining the following
models:
- model: mistralai/Mistral-7B-v0.1 # No parameters needed for base model
- model: WizardLM/WizardMath-7B-V1.1
parameters:
density: 0.65
weight: 0.4
- model: meta-math/MetaMath-Mistral-7B
parameters:
density: 0.6
weight: 0.3
merge_method: dare_ties
base_model: mistralai/Mistral-7B-v0.1
parameters:
int8_mask: true
dtype: float16
Then, for running the merge, run the following command:
mergekit-yaml config.yaml merge --copy-tokenizer --allow-crimes --out-shard-size 1B --lazy-unpickle
The merge took about 30 minutes to complete in the CPU instance within Google Colab. This depends on the amount and size of the models to merge, among other factors as the diversity of model families.
Note: this merging operations do not require GPU (although it can speed-up some operations). However, high-RAM could be required. Then, for evaluation we will need the GPU. So as an intermediate step to swap among a high-RAM and a GPU instance of the free tier in Google Colab, you could push your model to the Hugging Face hub. The result of this merge can be found in the following link: nachoaristimuno/MistralMath-7B-v0.1.
4.3 Evaluation
Now it is time to evaluate our model on the GSM8K dataset to compare the results. If we were using a CPU instance for the merge, switching to a GPU instance should be necessary due to the size of these models. First, we need to install the LM Evaluation Harness library for making the evaluation process easier.
git clone https://github.com/EleutherAI/lm-evaluation-harness cd lm-evaluation-harness pip install -e .
Next, we can run the following command for evaluating our new model:
lm_eval --model hf --model_args pretrained=nachoaristimuno/MistralMath-7B-v0.1,load_in_8bit=True --tasks gsm8k --device cuda:0 --batch_size 2
This will run the GSM8K evaluation benchmark using GPU (cuda:0) and a batch size of 2. If the model is not available locally, the command will download it directly from Hugging Face’s hub if it’s not found locally. Also, the load_in_8bit=True was set as the vRAM used for this evaluation was not enough loading the model in FP16. However, if you have enough vRAM you could take that configuration out.
4.4 Results
The results for the three models are shown below:
| Task | Version | Filter | n-shot | Metric | Value | Stderr | |
| gsm8k | 3 | strict-match | 5 | exact_match | 0.7015 | ± | 0.0146 |
| gsm8k | 3 | flexible-extract | 5 | exact_match | 0.7028 | ± | 0.0126 |
Results table for the model merge (nachoaristimuno/MistralMath-7B-v0.1)
| Task | Version | Filter | n-shot | Metric | Value | Stderr | |
| gsm8k | 3 | strict-match | 5 | exact_match | 0.7369 | ± | 0.0121 |
| gsm8k | 3 | flexible-extract | 5 | exact_match | 0.4996 | ± | 0.0075 |
Results table for the WizardLM/WizardMath-7B-V1.1 model
| Task | Version | Filter | n-shot | Metric | Value | Stderr | |
| gsm8k | 3 | strict-match | 5 | exact_match | 0.5912 | ± | 0.0106 |
| gsm8k | 3 | flexible-extract | 5 | exact_match | 0.5768 | ± | 0.0097 |
Results table for the meta-math/MetaMath-Mistral-7B model
In general, within the strict-match evaluation, the WizardMath models still performs better than the merge, and the merge performs better than the MetaMath model. However, in the case of the flexible-extract, the model merge outperforms both models.
In this case, the WizardMath is still one of the best performing models in the GSM8K benchmark, hence the difficulty of being able to surpass its performance. Nevertheless, our model merge is able to perform more consistently on both strict and flexible metrics.
5. Conclusions
Model Merging is gaining a lot of attention as it turns out to be a cheap and relatively easy way to create a model capable of different tasks by leveraging already trained models. Generally, these techniques involve computations with no need of GPU.
By leveraging some open source tools such as Mergekit, the process of experimenting different merges of models becomes easier. Just by looking for models which can be useful for our task and defining a merge configuration file, it could take less than an hour to test new models.
In our example case, we were able to create a new model merge by using two fine-tuned models on math datasets. By doing this, our new model outperforms one of the models in both exact and flexible metrics, and the other on the flexible-extract metric, but still a bit behind on the strict match-metric. An intuition we got by testing different model merges, is that this techniques becomes specifically useful when we want to allow a model to learn two different tasks from two different fine-tuned models. Although, it can still be useful when merging models fine-tuned on the same task.
These ways of creating new models out of already performing models will definitely become more common in 2024. Aligned with this, FrankenMoEs will probably become a trend due to the popularity of MoEs in the community and the release of different models which excel at particular tasks.
Last but not least, we explored the application of model merging within the context of LLMs. Nevertheless, these same concepts can also be applied to other groups of models, such as Diffusion Models within image generation.
6. References
- Model merging: Expanding the skills of LLMs on the go
- Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity
- Mixtral of experts blog
- LMSys Chat arena
- Mixtral of experts paper
- Mergekit repository
- Editing Models with Task Arithmetic
- Merge Large Language Models
- TIES paper
- DARE paper
- Model Merging: MoE, Frankenmerging, SLERP, and Task Vector Algorithms
- Merge Large Language Models with mergekit

