Exploring RetNet: The Evolution of Transformers

Since 2017, transformers have demonstrated their superiority in performance and computational efficiency, surpassing recurrent neural networks (RNNs). The attention mechanism introduced in the paper ‘Attention is All You Need’ and their ability to parallelize training—a feat traditional RNNs struggled with—attribute this superiority. However, transformers come with a challenge: the memory and inference costs associated with their architecture.

In this blog post we will explore the RetNet model, an initiative from Microsoft’s research team aimed at addressing the challenges posed by transformers while achieving competitive performance.

The predecessors: Recurrent Neural Networks and Transformers

Sequential processing in RNNs limits parallel training due to linear computations. RNNs process each token sequentially, hindering parallelization. Advanced RNNs, like LSTM and GRU, maintain a sequential flow, impeding efficient parallelization.

In contrast, Transformers introduce a paradigm shift by incorporating a self-attention mechanism. This mechanism, coupled with a ‘causal mask’ ensures that each token in a sequence has knowledge of all preceding tokens. The application of causal masking enables parallel training as each token can be processed concurrently, while maintaining a focus on its historical context. Consequently, every token functions as an independent training example, allowing Transformers to undergo training with all tokens simultaneously.

To summarize, Transformers overcome RNN limitations in sequential training. Attention mechanisms and causal masking make their training process more efficient and parallelizable. However, the self-attention mechanism poses challenges at inference and in memory usage, as detailed later.

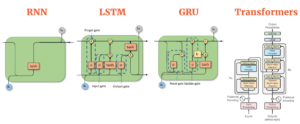
– Source: AIML- Compare the different Sequence models (RNN, LSTM, GRU, and Transformers)

Understanding the computations paradigms involved:

To understand the differences between recurrent and parallel computation, we will analyze a simple case. Given a linear equation:

ax + by + cz =👾 

How can this equation be computed in both a recurrent and parallel fashion? 

Recurrent Computation

The equation is broken down into smaller computations, each stored in a buffer (denoted as 𝛄).

1. First, ax is computed and stored in 𝛄.
2. Next, ax + by is computed by adding by to the existing buffer value and storing it back in 𝛄.
3. Finally, ax + by + cz is computed similarly, yielding the result 𝛄, which is equal to 👾.

This is a recurrent computation as it reuses the buffer 𝛄, accumulating data step-by-step through time. An RNN fundamentally accumulates data iteratively. Nonlinearities are usually associated with each step in an RNN. For instance, a sigmoid function σ(x) would accompany ax, by, and cz. This sequence must be computed first, preventing the possibility of parallelizing RNNs.

Parallel Computation

In parallel computation, the equation (a . x) + (b . y) + (c . z) =👾  can be calculated simultaneously:

(a)       (x)

(b)  (.)  (y) = 👾

(c)        (z)

Here, all terms are computed at once, making the process parallel.

The RetNet Approach

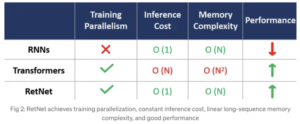
In architectures like Transformers, specifically designed for parallel computation, recurrent calculations are not possible. The softmax function introduces non-linearity, causing this limitation and requiring the addition of all terms before application. While softmax offers a crucial advantage for Transformers by providing relative attention weights and preserving long-term dependencies, it introduces a drawback. The computation of softmax (Q.Kᵀ) contributes to poor inference time performance, requiring the retention of softmax values in an NxN matrix that grows quadratically with sequence length, leading to increased memory demands.

– Source: Retentive Network: A Successor to Transformer for Large Language Models

RetNet introduces a foundational architecture for large language models, achieving training parallelism, cost-effective inference, and high performance. It addresses the limitation of transformers by omitting the softmax function, enabling both parallel and recurrent computation. Despite concerns about potential tradeoffs due to the loss of non-linear capabilities, research cited in this paper indicates that this change does not adversely affect performance and may even lead to improvements.

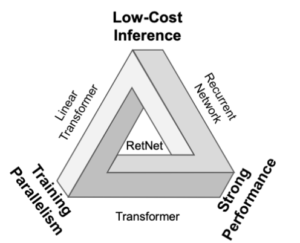
– Source: Retentive Networks (RetNet) Explained: The much-awaited Transformers-killer is here

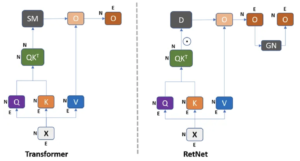
When comparing Transformer and RetNet models, both showcase training parallelization capabilities. However, a notable distinction arises in terms of inference cost. The Transformer incurs elevated expenses, necessitating the retention of the entire dataset in memory for successful inference, resulting in increased memory complexity in a quadratic manner for lengthy sequences. In contrast, the RetNet model accumulates data in a buffer, utilizing only the most recent buffer for the subsequent token in a recurrent manner.

– Source: Retentive Network: A Successor to Transformer for Large Language Models

(Green: RetNet | Grey: Transformers)

Retention 

The RetNet architecture introduces a novel concept called ‘Retention,’ defining it as follows:

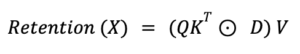
In this equation, Q, K, and V represent queries, keys, and values commonly found in attention mechanisms. The symbol (.) denotes element-wise multiplication, and RetNet introduces D as an additional matrix, serving as a gate or modifier to the attention mechanism.

Here’s a general explanation of what the equation does without diving into technical details:

The term QK^⊤ typically computes the similarities between queries and keys, acting as attention scores. D functions as a modulation factor, adjusting attention scores based on specific criteria or conditions. Finally, these adjusted attention scores are element-wise multiplied with V, the values, to produce the output, termed as ‘Retention.’

This innovative mechanism enables RetNet to perform both recurrent and parallel computations. The introduction of D introduces a new layer of complexity, allowing a balance between attention and other modifying factors.

By using this Retention mechanism, RetNet claims to maintain, or even enhance, the effectiveness of computations without relying on the softmax function. This ultimately allows for the parallel and recurrent processing of data, setting RetNet apart from traditional architectures like RNNs and fully parallel architectures like Transformers.

– Source: Retentive Network: A Successor to Transformer for Large Language Models

Parallel Representation of Retention 

The matrix D is defined as follows:

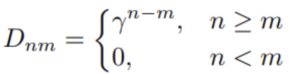
In this equation, γ is a scalar that decays as the time lag increases between n and m. In other words, the further back in time you go, the more the signal decays. This represents an improvement over a basic causal mask by integrating the concept of time decay, making the RetNet architecture more adaptable and proficient in capturing temporal dynamics. This time-decay factor plays a critical role in what the architecture calls “multiscale retention.”

The time-decay factor γ adds a layer of complexity and adaptability to the RetNet model. It allows the model to weigh recent tokens more heavily than older tokens, which is particularly useful in applications where the temporal sequence of data matters, such as time-series analysis or natural language processing. 

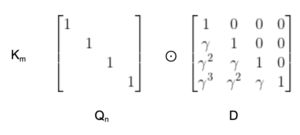
The diagram illustrates how the time-decay factor γ applies differently across various positions in the sequence, emphasizing the importance of recent data points and progressively reducing the weight as we move back in time.

Recurrent Representation of Retention

In the absence of the softmax function, the RetNet architecture enables a linear representation of the attention mechanism, facilitating recurrent computation during inference.

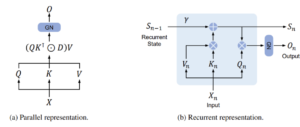
– Source: Retentive Network: A Successor to Transformer for Large Language Models

In practical terms, one can iterate through the sequence, accumulating data in a buffer—similar to how a recurrent neural network would. Diagrams that illustrate this process clearly highlight the distinction between parallel and recurrent representations. In the parallel representation, multiply all elements simultaneously, whereas, in the recurrent one, calculations proceed step by step. Within the recurrent representation, a recurrent state undergoes multiplication by a factor γ. Following this multiplication, another equation employs to compute the attention mechanism.

This equation, which would be unfeasible in traditional Transformer models, is then finally multiplied by the query to achieve the Retention mechanism.

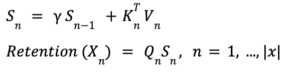
Essentially, the final output for each query in the sequence determines only after accumulating the associated keys and values through recurrent steps. In this manner, each token generates its queries and looks back at the sequence’s past, based on the key-value multiplications.

The recurrent representation allows for a more nuanced interaction with past sequences, proving particularly valuable in tasks requiring an understanding of temporal relationships or sequence dependencies. Unlike Transformers, RetNet efficiently handles these requirements through its recurrent representation, providing a unique advantage in a range of applications.

Chunkwise Recurrent Representation of Retention

The RetNet architecture introduces a clever ‘chunkwise’ operation, seamlessly combining recurrent computation with parallelism. The concept involves accumulating data in a buffer R, representing a ‘chunk,’ thus transforming the entire computation into a recursive process.

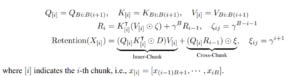
• Take the accumulated buffer from past chunks and compute it in parallel.
• Process the current chunk in parallel as well.
• Sum these two results together.

Essentially, “Junkwise” describes the strategy of aggregating information into an R-buffer, referred to as a ‘chunk,’ thereby introducing a recurrent nature to the process. This method harmonizes both recurrent and parallel approaches. Specifically, the distant past accumulates into a buffer using the recurrent form, while the immediate past or current chunk processes in a parallel manner.

This hybrid approach carefully balances recurrent and parallel processing. Consequently, this methodology enables the model to efficiently manage extensive sequences by swiftly accumulating information for long sequences into the buffer.

This technique empowers the model to “see” further into the past while retaining the advantages of parallel computation. By considering both the current and past chunks, the model can draw more intricate inferences from the data, proving highly efficient for tasks that require an understanding of long-term dependencies or sequences.

Gated Multi-Scale Retention

The RetNet architecture enhances its capabilities through ‘Gated Multi-Scale Retention’ (MSR), building on the earlier introduced time decay feature in the causal mask’s positional encoding. This concept aims to add nuance to the traditional multi-head attention mechanism used in conventional models.

• The model employs distinct γ values for each attention head, enabling diverse retention strategies. For instance, certain heads may focus on more recent tokens, while others attend to the entire sequence.
• Fix these γ values across different layers but vary them among heads, resulting in different attention dynamics.
• Introduce a swish gate to increase the layer’s non-linearity, enhancing the model’s representational power.

This concept, termed ‘gated multiscale attention,’ represents a nuanced enhancement of the traditional attention mechanism. By incorporating inherent time decay in position encodings and the causal mask, the authors introduce a sophisticated approach to attention.

In typical attention mechanisms, the system utilizes multi-head attention, transforming data into a larger query vector segmented into distinct parts. Each segment undergoes unique attention processing, and the results from individual ‘heads’ are consolidated. Building on this, the authors propose a modification: applying varying time decay factors to each head, allowing for adaptability in capturing a richer array of information and relationships within the data.

Overall Architecture of Retention Networks

The construction of an L-layer retention network involves stacking Multi-Scale Retention (MSR) layers and Feed-Forward Network (FFN) layers. This section explains the formal architecture of the L-layer model, highlighting its sequential transformation capabilities.

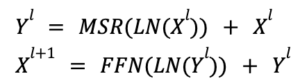
• MSR (Multi-Scale Retention): This handles the attention mechanism, allowing the network to focus on different parts of the input sequence.
• FFN (Feed-Forward Network): Acts as the computational backbone of the model, taking in the processed output from MSR and applying additional transformations.
• Layer Normalization (LN): Normalizes the layer outputs to stabilize the learning process and make the network more robust.

1. The alternating architecture of MSR and FFN allows the model to benefit from both specialized attention mechanisms and straightforward feed-forward computations.
2. Layer Normalization contributes to a more stable and efficient training process.
3. The formal structure is highly modular, meaning components can be tweaked or extended easily to adapt to various tasks and data types.

An L-layer retention network effectively integrates multi-scale retention and feed-forward networks, further fortified by layer normalization. This architecture is crafted to be both versatile and effective, making it well-suited for tackling complex machine learning tasks. In essence, you assemble a retention network by layering multi-scale retention and token-wise feedforward networks. At each stage, a residual connection is introduced, with layer normalization applied in between. This architecture bears resemblance to the transformer model, with the primary distinction lying in the substitution of the multi-head attention mechanism with multi-scale retention.

Experiments

Language modeling comparison

While the advancements, particularly in terms of inference, speed, memory, and latency, are noteworthy, it is essential to evaluate the architecture in language modeling tasks. In this context, the authors introduced metrics such as perplexity, zero-shot, and few-shot learning to substantiate RetNet’s claimed superiority. It’s important to note that, aside from a tutorial where a small ResNet is trained, there are no other resources available to showcase the model’s performance in these tasks.

Perplexity

The graph presents experimental results indicating that RetNet emerges as a robust competitor to Transformer for large language models. Empirically, RetNet begins to surpass Transformer when the model size exceeds 2B.

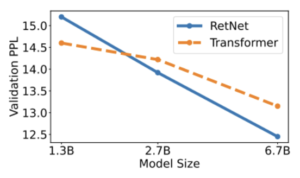
– Source: Retentive Network: A Successor to Transformer for Large Language Models

Zero-Shot and Few-Shot Evaluation on Downstream Tasks

By utilizing HellaSwag (HS), BoolQ, COPA, PIQA, Winograd, Winogrande, and StoryCloze (SC) as test datasets, the authors evaluated zero-shot and 4-shot learning with the 6.7B models. The accuracy numbers align with the language modeling perplexity reported earlier. RetNet demonstrates comparable performance to Transformer in zero-shot and in-context learning settings, as illustrated in the subsequent table.

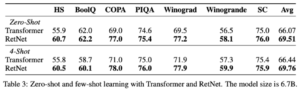
– Source: Retentive Network: A Successor to Transformer for Large Language Models

Training and Inference cost

Training cost

The table compares the training speed and memory consumption of Transformer, Transformer+FlashAttention, and RetNet, with the training sequence length set at 8192. Experimental results reveal that RetNet exhibits greater memory efficiency and higher throughput than Transformers during training.

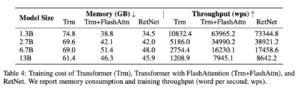
– Source: Retentive Network: A Successor to Transformer for Large Language Models

Inference cost

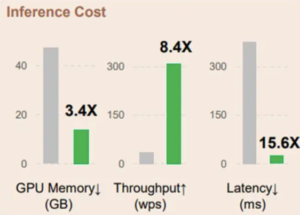
We measure the inference cost by comparing the memory cost, throughput, and latency. While the paper presents findings based on the 6.7B model tested on an A100-80GB GPU, for testing purposes we have experimented using this github repository. Due to memory limitations, we build the benchmark using a RetNet of 1.3B on a T4 GPU.

Memory: 

The memory cost of transformer increases linearly with sequence length due to KV caches. In contrast, the memory consumption of RetNet remains consistent around 4 GB even for long sequences requiring much less GPU memory to host RetNet. This makes RetNet more scalable and efficient for longer sequences.

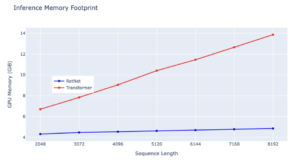
– Source: internal experiments

While both RetNet and Transformer are powerful architectures, RetNet’s consistent and low memory footprint makes it a more desirable choice for applications with constraints on computational resources, particularly for handling extensive sequences.

Throughput:

RetNet demonstrates a remarkable advantage in throughput over Transformer across all sequence lengths, showcasing its superior efficiency. While Transformer experiences a drop in throughput as decoding length increases, RetNet maintains a higher and length-invariant throughput by leveraging the recurrent representation of retention. Specifically, RetNet consistently achieves a throughput slightly above 150 tokens/s, underscoring its stable performance even with longer sequences. In contrast, Transformer’s throughput remains consistently low across various sequence lengths, consistently below 50 tokens/s. Both models exhibit throughput stability, but Transformer’s rate remains flat, whereas RetNet experiences minor fluctuations, highlighting RetNet’s overall efficiency in managing diverse sequence lengths.

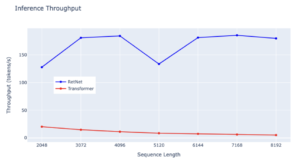
– Source: internal experiments

When evaluating the efficiency of these architectures in terms of inference throughput, RetNet emerges as the clear frontrunner. Its ability to process data at higher rates consistently, even with increasing sequence lengths, makes it a more suitable choice for tasks requiring rapid inference.

Latency: 

The latency of Transformers grows faster with longer input. Experimental results show that increasing batch size renders Transformer’s latency larger. Moreover, the latency of Transformers grows faster with longer input. By contrast, RetNet’s decoding latency outperforms Transformers and keeps almost the same across different batch sizes and input lengths.

– Source: internal experiments

Final thoughts

Initial experiments yield encouraging results. However, despite the current data suggesting that RetNet outperforms the Transformer across tasks, further insights might reveal specific domains where RetNet excels and others where it falls short. The preliminary data paints a rosy picture, yet achieving linearity in every process doesn’t necessarily guarantee universally stellar outcomes. If this were the case, it would revolutionize the field, offering a scalable architecture with minimal inference costs, enabling a myriad of optimization techniques due to its linearity, and potentially delivering enhanced performance. Nonetheless, arriving at such conclusions might be premature. The overall efficacy of the architecture, especially its emphasis on linear processes, remains a subject of further exploration.

For a deeper understanding of large language models (LLMs) and their implications, the article ‘An onboarding guide to LLMs‘ serves as a valuable resource, complementing the insights presented in this discussion.

References

• “Retentive Network: A Successor to Transformer for Large Language Models” https://arxiv.org/pdf/2307.08621.pdf 
• “Retentive Networks (RetNet) Explained: The much-awaited Transformers-killer is here” https://medium.com/ai-fusion-labs/retentive-networks-retnet-explained-the-much-awaited-transformers-killer-is-here-6c17e3e8add8
• A simple but robust PyTorch implementation of RetNet from “Retentive Network: A Successor to Transformer for Large Language Models” https://github.com/fkodom/yet-another-retnet