Intro to Mixed-Integer Linear Programming (MILP)

Introduction

Nowadays, when we think about solving complex problems with computers, immediately we think about big data and Machine Learning. Developing a Machine Learning solution usually requires an intensive amount of data, which we use to extract the patterns and rules that lie behind the behavior of our systems. But what happens when this data is not enough, or even worse, there is no available data at all? If we know those rules in advance, Mixed-Integer Linear Programming (MILP) might be the right choice.

MILP is a sub-area of the wider area called Convex Optimization, and it essentially involves two steps: modeling and optimization. Modeling a problem is the art of expressing a real-world scenario as a set of objective equations and constraints. The optimization process itself is related to finding the best possible solution for the objective taking into account the constraints. One can express and solve many of the usual problems in the industry through MILP. Maximizing a cash flow in the finance industry, finding the optimal route for a transportation problem, and finding an effective resource allocation for a manufacturing application, just to name a few.

In this blog, we dive into optimization practical applications. We begin by proposing a product allocation problem and modeling it using a MILP framework. This example will also allow us to explore some fundamental details of the MILP techniques, and finally, we implement the modeled problem in Python using the Pyomo library.

Mixed-Integer Linear Programming vs. Machine Learning

Although we can use Machine Learning (ML) and Mixed-Integer Linear Programming (MILP) to solve some of the same problems (sometimes in a complementary way) the approach is quite different. The typical Machine Learning pipeline starts with collecting and cleaning huge amounts of data, to then train a model that learns the underlying distribution of data to explain the real world. For MILP, we need to rely on experts to design a set of rules that explain the real world through mathematics. At first, it would seem that Machine Learning is a superior approach, as it can learn directly from data. However, when we do not have enough data, have clearly defined business rules, or want to be able to influence and modify the behavior of our system transparently, MILP shines.

Comparing the field of optimization to the cutting-edge developments in artificial intelligence, one might argue that optimization appears somewhat outdated. Since the late ’70s, mathematicians have been developing the optimization theory, especially the theory for Mixed-Integer Linear Programming. Although these methods have been around for quite some time, recent advances in optimization algorithms and raw computing power have made it possible to solve huge multivariate optimization problems with thousands (or maybe millions) of parameters in minutes. 

What can we solve with MILP?

There is a wide variety of problems that can be addressed with MILP, let’s dive into quick examples of some of them [1]:

💵 Cash flow optimization can be achieved by choosing which financial instruments to invest in and for how long according to our available capital to maximize return, or to minimize risk.

🛒 Product allocation is the process of allocating a variety of products to different shelves to maximize revenue. In the example we will allocate books of different sizes and prices to the available shelves, taking into account that some shelves get more visibility than others.

🏭 Resource allocation is the process of strategically allocating available resources to different tasks. In manufacturing, we would solve how to allocate the available workers and materials to our different production lines to maximize our total profit or minimize the total cost.

🕰️ Scheduling is similar to resource allocation but with temporality taken into account. Given a set of resources, we assign them to tasks in a given time. For example, if we need to assign workers to shifts, taking into account their availability and skills, we can compute the best possible schedule.

🛵 Route planning is what every food delivery company does. Given an origin and multiple destinies, choose the best route according to some criteria. Minimizing fuel consumption, minimizing average delivery times, or maximizing the number of delivered items in a given time.

✈️ Transportation networks are one of many applications of network flows. A transportation company that has to deliver goods from an origin city to a destination city, however, there are no direct flights between those cities. There are intermediate cities that can connect indirectly the origin and destination, but flights have different limits for how many goods they can transport. By modeling such a problem, we can maximize the number of goods that arrive at destiny from origin.

MILP basics

In this section, we will focus on Mixed Integer Linear Programming fundamentals. We will not go into much mathematical detail on the formulation, but we will provide a general context before jumping right into an application. We will also define some MILP lingo. 

Problem statement

Imagine we have an objective function called Y we need to optimize, for example, the total number of products in a product allocation. We have a set of parameters that contain prior fixed information for the problem, like product prices, sizes, shelf dimensions, and other fixed values. We need something we can tweak to achieve the optimum of our objective function. For this, we have decision variables, which represent any free variable that needs to be determined when solving the problem and are denoted with the letter x. For example, the positions for each of our products.

The possible values for the decision variables must verify a set of external, linear conditions called constraints. If we have M constraints that depend linearly on the decision variables we can formulate the problem as follows [2]:

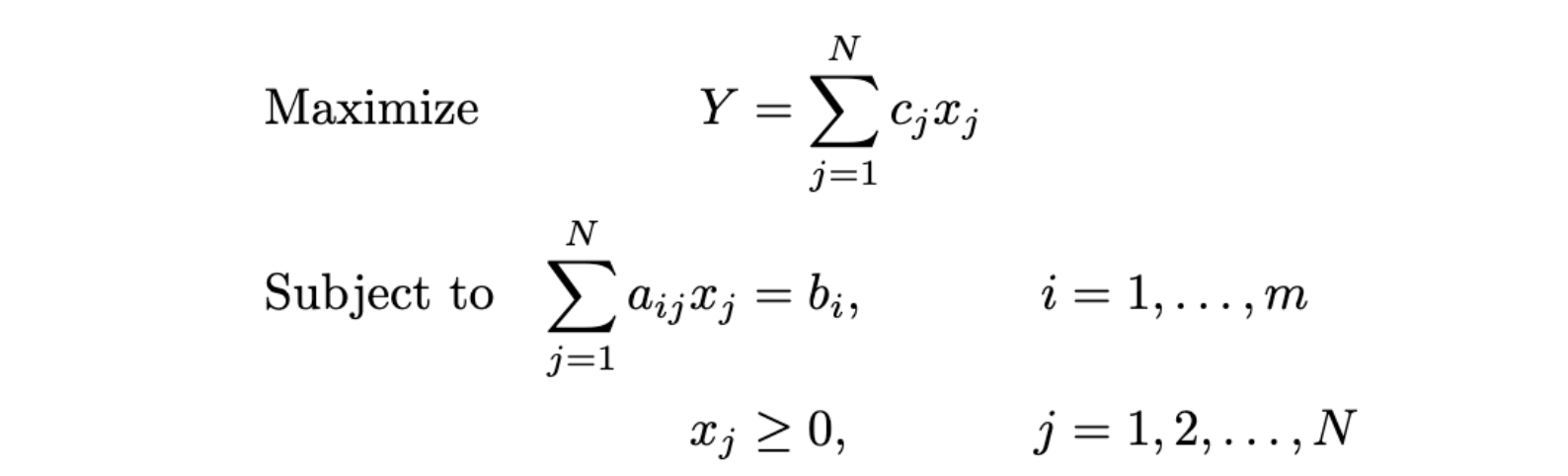
Solving this problem involves finding a set of values x that maximizes (or minimizes) the outcome Y. The constraints could be either equalities or inequalities and we could have an arbitrary number of them.

As mentioned earlier, this framework can model a wide variety of problems across different industries. Success in this area hinges on the ability to translate real-world scenarios into sets of equations. Next, we apply this framework to a product allocation problem.

Non-linear programming

This MILP formulation can be extended to other areas within Operations Research. If some of the constraints, or even the objective function, include some non-linearity, it is still possible to solve the optimization problem. This requires the application of a different set of techniques, known as Mixed Integer Non-Linear Programming (MINLP).  However, one might also use traditional MILP techniques by approximating non-linear variables by linearizing them on the interval of interest. This would logically lead to approximate solutions, but in most cases, these solutions are good enough for the application problems. 

Optimization into practice: Product allocation

An online bookstore wants to open its first physical store, and one of the challenges it faces is how to place books on bookshelves to maximize revenue. To solve this, they chose to contact us, optimization wizards, to help fix their problem. We summed up their requirements into the following statement:

We need to fit as many books as we can on the bookshelves while putting the most popular books on the most visible shelves, and while keeping the same authors close together.

As mentioned in the previous section, we need to identify parameters, variables, constraints, and objective function, so that we can then find the optimal solution. It is common practice to define these components of the solution verbally to then formulate them mathematically.

Parameters: For each book, we need a measure of its popularity, price, author, and dimensions. In turn, for each shelf within the bookshelves, we need to know the dimensions and the visibility or exposure they provide to the books.

Variables: For each book, we need to know on which shelve, and on which place within that shelf it should be located.

Constraints: We must only include one copy of each book, and they must fit into the shelf by height. The total length of the selected books on a shelf must fit on the bookcase width. Also, books from the same author must be on the same bookcase.

Objective Function: The revenue of each book is defined by the book’s price, its popularity, and the visibility its location provides. Our objective is to maximize the total revenue, as the sum of the revenue of all allocated books.

Sets

First, we define the set of indices that we will use for defining our problem. As we will have many variables and parameters that repeat for each book, bookcase, and author, indexes make notation much easier.

• The set B represents the set of books considered for the problem. Each individual book will be referred with the subindex b.
• The set C represents the set of bookcases considered for the problem. Each individual bookcase will be referred with the subindex c.
• The set A represents the set of authors considered for the problem. Each individual author will be referred with the subindex a.
• The set S represents the set of shelves considered for the problem. Each individual shelf will be referred with the subindex s.

Parameters

Then we define the problem’s parameters, which represent prior information and configurations, so values that we cannot tweak in our optimization process:

Books

• We define the parameter b_pop_b as the popularity of book b.
• We define the parameter b_widthh_p as the width in mm for book b.
• We define the parameter b_height_b as the height in mm for book b.
• We define the parameter b_price_b as the price in USD for book b.
• We define the boolean parameter is_author_a,b which is true if book b was authored by author a and false if not.

Bookcases

• We define the parameter s_width_c,s as the width in mm for shelf s from bookcase c.
• We define the parameter s_height_c,s as the height in mm for shelf s from bookcase c.
• We define the parameters s_visibility_c,s as the visibility a book gains from being positioned on shelf b from bookcase c.

Decision Variables

Next, we should identify the decision variables whose values must be found in the optimization process. These variables represent all the values we can tweak as practitioners:

• We define the boolean variable  Is_Book_At_b,c,s which represents if book b is in shelf s of bookcase c.
• We define the boolean variable Is_Author_At_a,c,s which represents if author a is in shelf s of bookcase c.

Constraints

Now, having defined the decision variables, we need to mathematically define all the problem’s constraints. Our first constraint is related to limiting the number of times we can allocate a book.

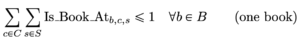
In this way, we make sure that each book is allocated at most once, also allowing the model to leave out books if they do not fit. 

Two constraints have to do with the size of the shelves: 

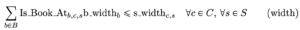
To limit the number of bookcases an author appears in, we need to fill up the accessory variable Is_Author_At_a,c,s. This can be done by the combination of two constraints. 

Then we need to make sure that each author appears in at most one bookcase:

Objective Function

Finally, we need to define the objective function that we are trying to maximize. In this case, the expected revenue of a specific disposition of books:

After formulating the problem, solving it becomes a matter of utilizing standard linear programming solvers. There are many open-source solvers such as GLPK from GNU, GLOP, and CP-SAT developed by Google, and many more.

Product allocation optimization using Pyomo

Now that the problem is completely defined, it is time to implement it using Pyomo [3], a Python-based open-source library that supports a diverse set of optimization capabilities for solving optimization models. Although we will leverage it for solving a linear problem, it also has non-linear capabilities for solving more complex problems.

Now it is time to start filling up our bookcases!

Dataset

To work on our problem, we need book data. We will work with a dataset of Fantasy books (inspired by this dataset). It includes book features like dimensions, author information, and average sales. A book’s popularity can be inferred by their average sales.

Then we then need to measure our imaginary bookcases to define the available space for books. For this example, we will work with 3 bookcases, 5 shelves each, with 1 meter of width and tall enough to store the tallest. Each shelf also has its own visibility factor, a multiplier on book sales as we position them on this shelf. Let’s take a look at the data we will feed the model.

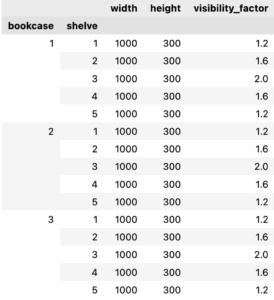
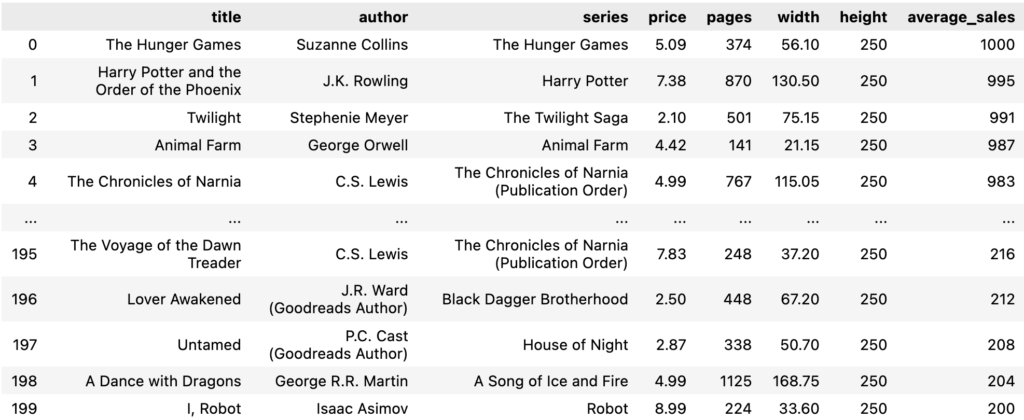
Model

Parameters

One interesting feature of Pyomo is that it allows us to define model variables and parameters in a functional way. Using the notation defined in the previous section we have our sets:

# Define the sets 
model.B = pyo.Set(initialize=book_ids, doc="Books")
model.S = pyo.Set(initialize=shelf_ids, doc="Shelves")
model.C = pyo.Set(initialize=bookcase_ids, doc="Bookcases")
model.A = pyo.Set(initialize=author_ids, doc="Authors")   

And our parameters:

# Define the parameters 
model.b_width = pyo.Param(
    model.B,
    initialize=lambda model, b: book_widths[b],
    within=pyo.NonNegativeReals,
    doc="Width of book b",
)
model.b_height = pyo.Param(
    model.B,
    initialize=lambda model, b: book_heights[b],
    within=pyo.NonNegativeReals,
    doc="Height of book b",
)
model.b_pop = pyo.Param(
    model.B,
    initialize=lambda model, b: book_average_sales[b],
    within=pyo.NonNegativeReals,
    doc="Average sales of book b",
)
model.b_price = pyo.Param(
    model.B,
    initialize=lambda model, b: book_prices[b],
    within=pyo.NonNegativeReals,
    doc="Price of book b",
)
model.is_author = pyo.Param(
    model.B,
    model.A,
    initialize=lambda model, b , a: 1 if author_per_book[b] == a else 0,
    within=pyo.Binary,
    doc="Is a author of book b",
)
model.s_height = pyo.Param(
    model.S,
    model.C,
    initialize=lambda model, s, c: shelf_heights[c,s],
    within=pyo.NonNegativeReals,
    doc="Height of shelf s in bookcase c",
)
model.s_width = pyo.Param(
    model.S,
    model.C,
    initialize=lambda model, s, c: shelf_widths[c,s],
    within=pyo.NonNegativeReals,
    doc="Width of shelf s in bookcase c",
)
model.s_visibility_factor = pyo.Param(
    model.S,
    model.C,
    initialize=lambda model, s, c: shelf_visibility_factor[s],
    doc="Visibility factor of shelf s in bookcase c",
)

This way, we are telling Pyomo that widths and heights are parameters with B components and that the shelf parameters have S times C components, one for each shelf in each bookcase. This formulation is quite useful since it allows us to modify the input dimension without changing this piece of code.

Decision Variables

Now, we define the decision variables and force our decision variables to be binary.

# Define the variables 
model.Is_Book_At = pyo.Var(model.B, model.S,model.C, domain=pyo.Binary) 
model.Is_Author_At = pyo.Var(model.A, model.C, domain=pyo.Binary)

Constraints

Next, we add all constraints to the model. In Pyomo, one can define the constraints using regular Python functions. These functions must return a boolean value based on a condition on the parameters and variables. 

We first define all functions:

def __width_rule(model, s, c):
    return (sum(model.Is_Book_At[b, s, c] * model.b_width[b] for b in model.B)
        <= model.s_width[s, c])

def __height_rule(model, s, b, c):
    return ( model.Is_Book_At[b, s, c] * model.b_height[b] <= model.s_height[s, c])
def __max_books_rule(model, b):
    return sum(model.Is_Book_At[b, s, c] for s in model.S for c in model.C) <= 1

def __author_in_bookshelve_rule_1(model, b, a, s, c):
    return (model.Is_Author_At[a, c]
        >= model.Is_Book_At[b, s, c] * model.is_author[b, a])

def __author_in_bookshelve_rule_2(model, a, c):
    return model.Is_Author_At[a, c] <= sum(model.Is_Book_At[b, s, c] * model.is_author[b, a]
        for b in model.B
        for s in model.S)

def __max_bookshelves_author_rule(model, a):
    return sum(model.Is_Author_At[a, c] for c in model.C) <= 1

And then define the constraints:

# Define the constraints
model.width_constraint = pyo.Constraint(model.S,model.C, rule=width_rule, doc = "All books in shelf together should be less than shelf width")
model.height_constraint = pyo.Constraint(model.S, model.B, model.C, rule=height_rule, doc = "Books should be less tall than shelf height")
model.max_books_constraint = pyo.Constraint(model.B,rule=max_books_rule, doc = "Each book should be in only one shelve")
model.author_in_bookshelve_constraint_1 = pyo.Constraint(model.B,model.A,model.S, model.C, rule=author_in_bookshelve_rule_1, doc = "Fill if author is in bookshelve")
model.author_in_bookshelve_constraint_2 = pyo.Constraint(model.A, model.C, rule=author_in_bookshelve_rule_2, doc = "Fill if author is in bookshelve")
model.max_bookshelves_author_constraint = pyo.Constraint(model.A, rule=max_bookshelves_author_rule, doc = "Each author should be in only one bookshelve")

Objective Function

The final ingredient in our model is the objective function.

# Objective function
def objective_function(model):
    total_books_earnings = sum(
        model.Is_Book_At[b, s, c]
        * model.b_price[b]
        * model.b_pop[b]
        * model.s_visibility_factor[s,c]
        for b in model.B
        for s in model.S
        for c in model.C
    )
    return total_books_earnings

model.cost = pyo.Objective(rule=objective_function, sense=pyo.maximize)

Solving the model

Now we can finally solve the model:

# Select solver and solve
solver = pyo.SolverFactory('glpk')
solution = solver.solve(model)

Let’s check how we did on modeling the problem. The image below shows how books were located on the bookcases, in orange we highlighted books by J.K Rowling, to show that same-author books are in the same bookcase.

We can see that books fit well on the bookcases, with little to no space to spare. Also, thin books with higher width/prices are located in the middle shelves, the most visible regions of the bookcase, while thicker and less expensive books are located towards the bottom shelves. The following table sums up some statistics about the results.

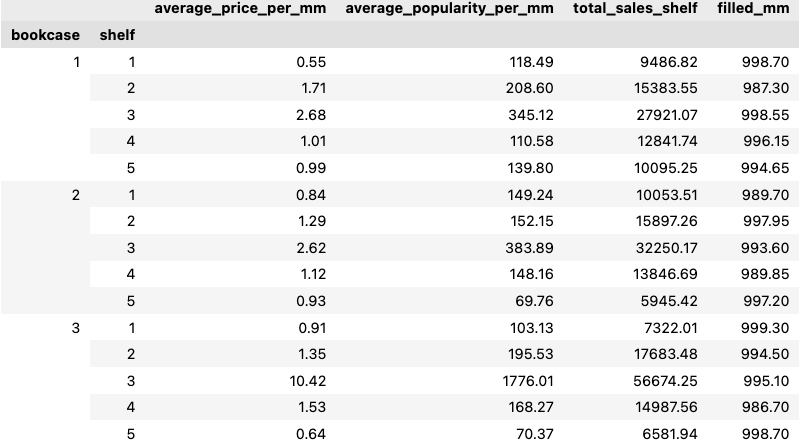
What would happen if we had less books? Let’s run the model again, but remove some of the least popular books from the input list.

As expected, the model chooses to leave empty spaces on one of the least visible shelves. Putting a book there instead of on a shelf with higher visibility would go against the model objective.

Can we always obtain an optimal solution?

When looking at LP or MILP formulations, we see that the constraints impose some restrictions on the possible values for the decision variables. There are combinations of values that will not meet the restrictions, and therefore will not be optimal candidates. Formally, one can evaluate the feasibility of the optimization problem for MILP with the Karush–Kuhn–Tucker (KKT) conditions. For the sake of simplicity, we will not go into that in this post.

The set of all combinations of decision variables that satisfy all constraints is called the feasible region, and solving a linear programming problem involves finding the maximum (or minimum) value of an objective function inside this feasible region.

Feasible and bounded solutions

To visualize this feasible region, imagine we have two non-negative decision variables x1 and x2, and a set of constraints. We could represent the problem in a two-dimensional plot as below:

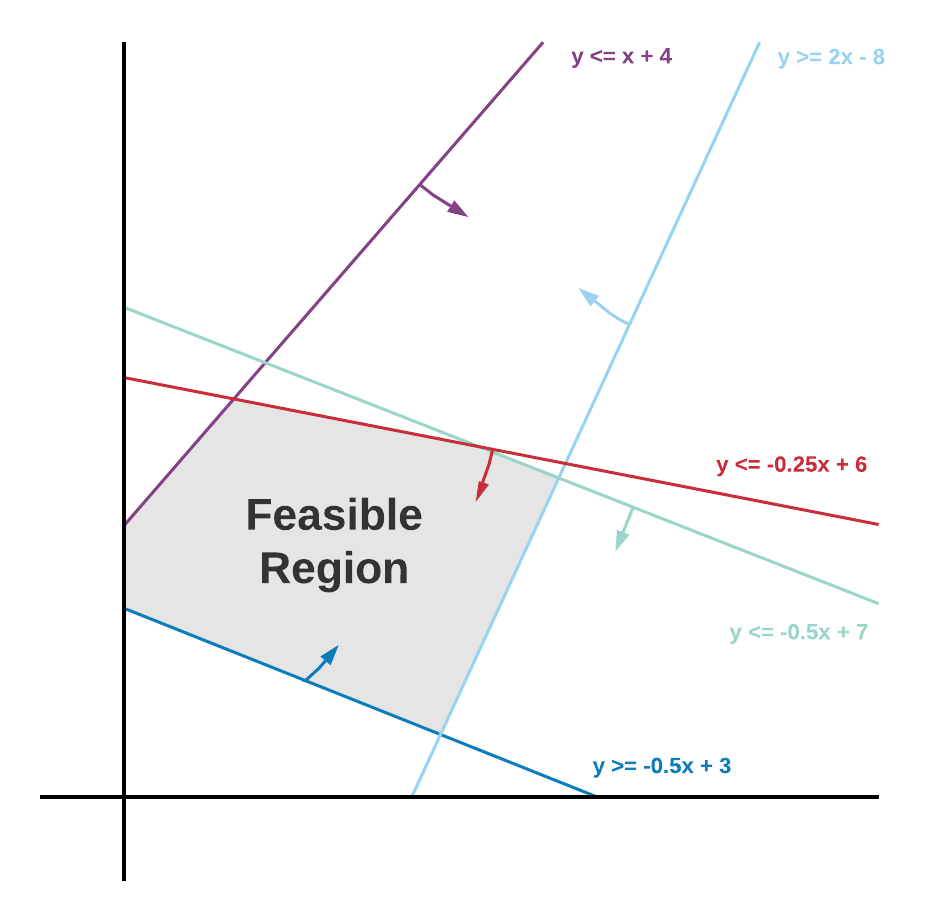
Infeasible or unbounded solutions

Our problem might involve a bounded feasible solution like in the image above, but this region could also be infeasible or unbounded. Infeasible regions appear when there are no combination of variables that can satisfy all constraints at the same time. Unbounded regions appear when the feasible area is infinitely large. The image below shows a difference between these scenarios:

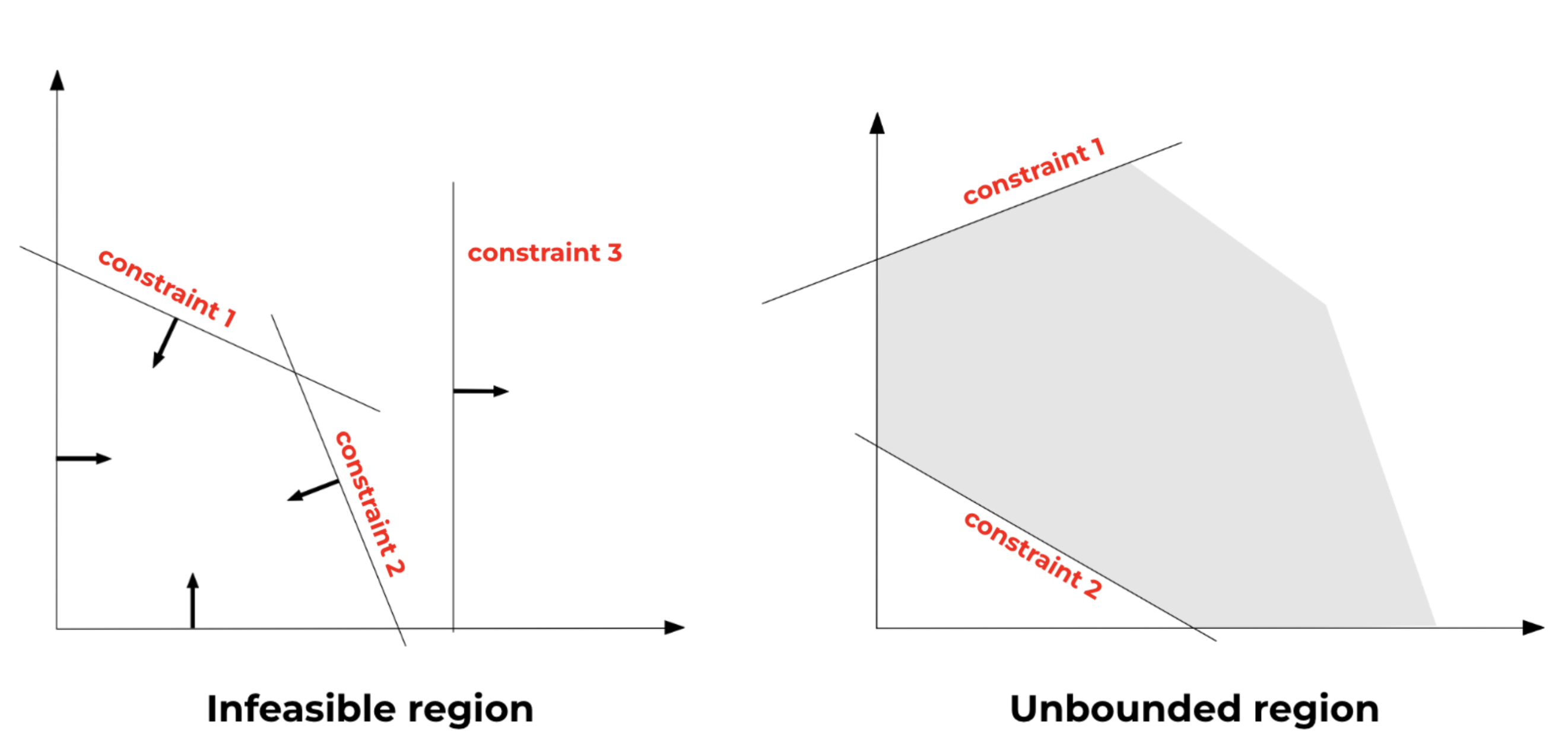
• Optimal solution: in this case, the problem is well-defined and it is possible to find an optimal value of the objective function within the feasible region.

• Unbounded solution: whenever the function to maximize (minimize) can grow (decrease) infinitely within the feasible region, for example if the feasible region is not completely enclosed. 
• Infeasible solution: if the feasible region does not exist, the problem does not have a feasible solution.

Usually getting infeasible or unbounded solutions is an indicator of an ill-defined problem. In our example, without limiting the bookcase width, we would have achieved infinite books allocation although they would not fit in the shelves.

Conclusions

In this post, we dived into the world of Mixed-Integer Linear Programming for solving an optimization problem. Specifically, we modeled a product allocation problem as an example using the open-source library Pyomo. Modeling problems in such a way is a powerful and useful approach, especially when little or no data is accessible.

Creating a robust model that represents reality usually requires a deep understanding of the underlying problem and some industry-relevant expertise. A lot of bibliography exists on this topic, and most of the usual problems have already been solved. As a first step, it is a good practice to refer to a specialized bibliography before trying to reinvent the wheel.

References

1. OR-Tools for Python
2. MOSEK Cookbook on linear optimization
3. Pyomo documentation
4. Linear programming and Optimizer blog from Anapedia
5. AIMMS Optimization Modeling manual